Last time I wrote that I could not show an animation of a cloakfish, because it had been saved as a gif. Well, I could not resist to do one again. As I wanted to take advantage of a faster computer, I adapted the file to result in two cloakfish instead of one; a young? The male? I originally wished to change the relative sizes of body to tail in the small animal, so the body would exhibit 'allometric' growth, meaning some body parts of the young have a disproportionate size, such as large heads and large eyes in human children. That turned out to be trickier than I thought, so now the animal grows isometrically: infants are pure downscaled versions of the adults. I did however adapt the speed at which the smaller one moves its tail membranes, and its body movement now is less sedate as well due to less inertia. As a result, the animation definitely shows results of the difference in size between the two animals.
I also changed the phase differences of the four cloaks from the earlier one, so the animal is in fact using a different 'gait'. There is more of that on the website, to be found in the 'water' page, under 'swimming with membranes'.
The video above shows the result, but at a low resolution. Oddly, the width to height ratio is no longer correct (the image should be a bit wider). Perhaps I should have stuck to a 4x3 ratio instead of going for 720x480 pixels. I am not very familiar with all the various video formats. I did manage to add some titles though, and copied the idea for the soundtrack from an animation I showed earlier. I think I will put this animation up on the Furaha site; meanwhile, as an experiment, I also put it up on YouTube as an experiment. The image ratio turmed out better there...
Saturday, 31 July 2010
Sunday, 25 July 2010
Furahan Fossils
While it might be nice to design fossils of life forms that never existed, that is not what this post is about. The 'fossil' part of the title concerns bits of the Furaha website that once existed but later vanished in an upheaval of sudden changes, and slowly got forgotten afterwards. This happened to the GalFloat advertisements and to several life forms. Some were and are perfectly viable, and are taken off the site simply to keep enough unpublished data for the eventual book. But some disappeared because they were no longer good enough, and some of these will be resurrected here. That happened to 'amphorae' and 'colonies', life forms in clear seas. They first appeared on the Furahan stage somewhere around 1997.
The life forms in questions were shown as animations, and as such they were subject to changes in computer hardware. They were originally written in QBasic, that used to come bundled with Windows. The Basic programs produced length text files defining large numbers of triangles as coordinates in space, and these text files were in turn read by a free program called 'Persistence of Vision' (POV), a ray-tracer. I used that to animate one image at a time, and a day or so later I had a long list of images numbered sequentially. These were then used to form an animation in the form of a .gif file. There were major hurdles in this laborious process: the first was that QBasic programs quickly looked daunting, limiting the complexity of the scenes. The major hurdle was of course the internet: the animations had to be short and small at only 75x125 pixels. Even then loading them took quite a while.
Time passed, the internet sped up, and at one point in time I considered the animations too small and too tiny to keep on the site. Then I found out that I had not kept all original Basic files. Extinction.
More time passed, and I stumbled on a CD with the missing programs. Still not all of them, but together the fossils allowed a fairly good look at these erstwhile life forms. So I found a new incarnation of QBasic, found that POV still existed, and went to work. The animations are bigger and include more complex scenes, but essentially they show the same things their ancestors did.
An amphora as shown in QBasic. Mind you, you have
to program things such as a perspective
transformation yourself in Basic! Click to enlarge.
Here is one: a scene showing amphorae. At the time, I had not stipulated why they moved the way they did, but a reader came up with a suggestion: they did so to avoid amphorivores. By the way, that reader had at the time chosen the name Nemo, but had not settled on 'Ramjet' yet). The amphorae used to sway a bit with the current; that part seems to have been lost for eternity.
And another one: a colony thingy. I remember that all the globes you see here are part of one and the same organism, but do not remember what the parts were for. They were probably just there to make it look interesting.
Click to enlarge; copyright Gert van Dijk
The image above was supposed to be animated as well; it is of course a cloakfish. Now cloakfish did not go extinct on my site, but are in fact thriving. The corresponding programs were about the only ones that remained to be resurrected when the others all went extinct. Why is the image above not animated? Because it was saved as a .gif file, and this blogger program seems to dislike that. Computer progress: three steps forward, one backwards and one sideways.
The reason for such a laborious production process was that it was the only one I could think of that would allow me to show the type of shape changes I wanted to have. I still do not think that there is a readily available 3D-program that would allow me to produce shapes such as the cloakfish tail with some ease. The downside of course is that I could not add a suitable-looking landscape. As you can see, the bottom of the sea in these animations is completely flat. It would be nice to make use of the features that a modern 3D programs such as Vue Infinite provides. If I could just find a way to reliably control the position of an imported object, I would be ready for the next evolutionary era. That's one of the reasons there are as yet only schematic animations of flying tetropters, instead of nicely rendered ones. Meanwhile, the Furahan fossils shown here will probably remain extinct for the time being.
An amphora as a 'patch' in Matlab. The user
provides the 3D-coordinates, and the display
is dealt with by the program. Progress!
Still, I could not resist porting the amphora shape definition routines to Matlab, which was not difficult (learning a language takes time, using it does not). I then used an old routine to translate Matlab's 'patch' into a common 3D format (obj), and then I imported a few amphorae into a Vue seascape to show what the result might be like. Here it is, at the end of a post, waiting for life to arrive.
Click to enlarge; copyright Gert van Dijk
The life forms in questions were shown as animations, and as such they were subject to changes in computer hardware. They were originally written in QBasic, that used to come bundled with Windows. The Basic programs produced length text files defining large numbers of triangles as coordinates in space, and these text files were in turn read by a free program called 'Persistence of Vision' (POV), a ray-tracer. I used that to animate one image at a time, and a day or so later I had a long list of images numbered sequentially. These were then used to form an animation in the form of a .gif file. There were major hurdles in this laborious process: the first was that QBasic programs quickly looked daunting, limiting the complexity of the scenes. The major hurdle was of course the internet: the animations had to be short and small at only 75x125 pixels. Even then loading them took quite a while.
Time passed, the internet sped up, and at one point in time I considered the animations too small and too tiny to keep on the site. Then I found out that I had not kept all original Basic files. Extinction.
More time passed, and I stumbled on a CD with the missing programs. Still not all of them, but together the fossils allowed a fairly good look at these erstwhile life forms. So I found a new incarnation of QBasic, found that POV still existed, and went to work. The animations are bigger and include more complex scenes, but essentially they show the same things their ancestors did.
An amphora as shown in QBasic. Mind you, you haveto program things such as a perspective
transformation yourself in Basic! Click to enlarge.
Copyright Gert van Dijk
Here is one: a scene showing amphorae. At the time, I had not stipulated why they moved the way they did, but a reader came up with a suggestion: they did so to avoid amphorivores. By the way, that reader had at the time chosen the name Nemo, but had not settled on 'Ramjet' yet). The amphorae used to sway a bit with the current; that part seems to have been lost for eternity.
Copyright Gert van Dijk
And another one: a colony thingy. I remember that all the globes you see here are part of one and the same organism, but do not remember what the parts were for. They were probably just there to make it look interesting.
Click to enlarge; copyright Gert van DijkThe image above was supposed to be animated as well; it is of course a cloakfish. Now cloakfish did not go extinct on my site, but are in fact thriving. The corresponding programs were about the only ones that remained to be resurrected when the others all went extinct. Why is the image above not animated? Because it was saved as a .gif file, and this blogger program seems to dislike that. Computer progress: three steps forward, one backwards and one sideways.
The reason for such a laborious production process was that it was the only one I could think of that would allow me to show the type of shape changes I wanted to have. I still do not think that there is a readily available 3D-program that would allow me to produce shapes such as the cloakfish tail with some ease. The downside of course is that I could not add a suitable-looking landscape. As you can see, the bottom of the sea in these animations is completely flat. It would be nice to make use of the features that a modern 3D programs such as Vue Infinite provides. If I could just find a way to reliably control the position of an imported object, I would be ready for the next evolutionary era. That's one of the reasons there are as yet only schematic animations of flying tetropters, instead of nicely rendered ones. Meanwhile, the Furahan fossils shown here will probably remain extinct for the time being.
An amphora as a 'patch' in Matlab. The userprovides the 3D-coordinates, and the display
is dealt with by the program. Progress!
Still, I could not resist porting the amphora shape definition routines to Matlab, which was not difficult (learning a language takes time, using it does not). I then used an old routine to translate Matlab's 'patch' into a common 3D format (obj), and then I imported a few amphorae into a Vue seascape to show what the result might be like. Here it is, at the end of a post, waiting for life to arrive.
Click to enlarge; copyright Gert van Dijk Sunday, 18 July 2010
Size matters, but so does gravity II
In a previous post on scaling I tried to explain why you cannot simply double all size measures of an animal if you want to make it bigger. Leg bones in particular should become more than twice as thick. The reason was that doubling an animal's length, height and width will make it weigh not two but eight times as much. To withstand the eightfold increase in weight the cross section of the leg bones has to become eight times larger, instead of four times, which is what you get if you merely double the diameter. The wanted diameter change is obtained by taking the square root of how much the cross section has to change. The square root of 8 is 2.82, so there we are.
All that held for altering an animal's size on one and the same planet; but what happens if the animal's size is kept the same, but it is transferred to a world with a different gravity? This is easy: the leg bones once again have to withstand the weight of the animal, so the question is how much that changes under the influence of another gravity. Weight is a force: it is the product of the gravitational acceleration g and the object's mass. From that it follows that weight is directly proportional to the value of g, and that value depends on the planet; Earth's gravity is taken as the standard, so it is at 1g. Transporting a animal of any given weight to a 2g world will double that weight, and being on a 3g world will triple it, etc. To adapt its bones to these new environments, their cross section will have to become twice as large on a 2g world, three times as large on a 3g world, etc. What that means for the diameter of the bones is not difficult to work out: for the 2g world the original diameter has to multiplied by the square root of 2, which is 1.41, and for the 3g world the value would be the square root of 3, or 1.73.
Click to enlarge; copyright Gert van Dijk
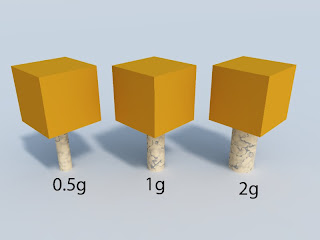
The picture above shows a mass on a cylinder. The diameter of the cylinder is just right to support the weight of the cube. The cubes are thought to stand on three different worlds, with 0.5g, 1g and 2g. The cylinders have been changed to make them right for each world, so their diameters are 0.70, 1, and 1.41.
Click to enlarge; copyright Gert van Dijk
For the mathematically inclined here is the relationship between body size, leg bone diameter and gravity, all together. The change in overall size you want to achieve is given on the x-axis (so '3' means the animal's height, length and width are all to become three times the original size), and the y-axis shows by how much you have to multiply the original leg bone diameter to obtain the new one. The three blue lines give the relationship for three different values of g. Suppose that your animal will run into trouble if the bone diameter increases beyond four times, for instance because too much of the animal will be bone! The graph shows that you reach that diameter value when the size increases a bit more than two times on a 2g world, but on a 0.5g world the animal can become more than three times the original size. So you can have animals with thin bones on a heavy planet, but they just have to be rather smaller than animals with similar bones on a low-gravity planet.
Click to enlarge; copyright Gert van Dijk
Finally here is the cartoon doggie (Disneius caniformis) adapted to three different worlds. Of course, there are other things to take care of when designing life forms for worlds with different gravities. While an animal's weight changes by transporting it to another world, its mass does not, and its inertia does not either. Muscle mass will need to be changed as well, as withstanding a greater weight will require larger muscles. Leg position may have to be changed as well. The more difficult it is to counter a high weight, the more likely it is that the legs will be kept vertically, i.e., without major angles between the bones. The difficulty in question depends both on an animal's mass and on local gravity. Mind you, there is more to be said on leg bending, as well as on leg splaying; the two are not the same thing, but perhaps that is something for another post.
PS. It seems to be getting more difficult to find new interesting speculative biology projects out there that aren't well-known already. I have my eye on one, but suggestions are welcome.
All that held for altering an animal's size on one and the same planet; but what happens if the animal's size is kept the same, but it is transferred to a world with a different gravity? This is easy: the leg bones once again have to withstand the weight of the animal, so the question is how much that changes under the influence of another gravity. Weight is a force: it is the product of the gravitational acceleration g and the object's mass. From that it follows that weight is directly proportional to the value of g, and that value depends on the planet; Earth's gravity is taken as the standard, so it is at 1g. Transporting a animal of any given weight to a 2g world will double that weight, and being on a 3g world will triple it, etc. To adapt its bones to these new environments, their cross section will have to become twice as large on a 2g world, three times as large on a 3g world, etc. What that means for the diameter of the bones is not difficult to work out: for the 2g world the original diameter has to multiplied by the square root of 2, which is 1.41, and for the 3g world the value would be the square root of 3, or 1.73.
Click to enlarge; copyright Gert van DijkThe picture above shows a mass on a cylinder. The diameter of the cylinder is just right to support the weight of the cube. The cubes are thought to stand on three different worlds, with 0.5g, 1g and 2g. The cylinders have been changed to make them right for each world, so their diameters are 0.70, 1, and 1.41.
Click to enlarge; copyright Gert van Dijk
Click to enlarge; copyright Gert van DijkFinally here is the cartoon doggie (Disneius caniformis) adapted to three different worlds. Of course, there are other things to take care of when designing life forms for worlds with different gravities. While an animal's weight changes by transporting it to another world, its mass does not, and its inertia does not either. Muscle mass will need to be changed as well, as withstanding a greater weight will require larger muscles. Leg position may have to be changed as well. The more difficult it is to counter a high weight, the more likely it is that the legs will be kept vertically, i.e., without major angles between the bones. The difficulty in question depends both on an animal's mass and on local gravity. Mind you, there is more to be said on leg bending, as well as on leg splaying; the two are not the same thing, but perhaps that is something for another post.
PS. It seems to be getting more difficult to find new interesting speculative biology projects out there that aren't well-known already. I have my eye on one, but suggestions are welcome.
Wednesday, 7 July 2010
To cernuate or not to cernuate... (cernuation III)
It would appear that my previous explanation of cernuation left something to be desired, so I will try again. When I coined the word, I was thinking about a mode of locomotion invented by the people responsible for 'The Future is Wild' (TFIW). The squibbons, descendants of cephalopods, have taken to the trees and swing from branch to branch from their tentacles. That could be just what a tentacle might be good at, as it mostly involves tensile forces; tentacles are not well fit to withstand compressive forces needed for walking.
Brachiation is what comes to mind when gibbons or monkeys swing from branch to branch: they hang from one arm while the other swings to grab another branch. While they do so the body stays largely upright, meaning the head is always above the feet.
The way squibbons do this, cernuation, has similarities: the animal swings suspended from one or more arms while other arms move forward to grab a new branch. But the movement is like an inverted somersault, so, while one swing sees the head upwards, the next has it downwards. I presented a fragment of 'TFIW' showing a squibbon moving that way, but the lighting was not very even so the movement may not have been well visible. This post rectifies that.
Click to enlarge; copyright Gert van Dijk
Above you see a rough model of a cernuator. It is only a simple ZBrush model, not meant as a proper animal (I hope my ZBrush friends will forgive me). The animal has very long eye stalks, long arms and long legs, and the head is kept downwards so the eyes stay near the centre of the body; the body is even bent to make room. Having the eyes near the centre was borrowed from the squibbon; this particular concept is stressed in the book 'TFIW'. The idea is probably that this eye position minimises the vertical distance the eyes travel over during cernuation. We'll get back to that.
Click to enlarge; copyright Gert van Dijk
This image shows part of the movement cycle, starting when the body hangs vertically from the arms, and ending where the animal can grasp another branch with its feet.
Click to enlarge; copyright Gert van Dijk
The next diagram starts at the same stage, and ends at the point where the hands are ready to grasp a branch. Note that the animal is upside down during this part of the movement, and moves with its back towards the direction of swing.
Click to enlarge; copyright Gert van Dijk
And finally the animal swings from its hands right up to the point where the cycle began. Notice that the body is now right side up again, and the back faces, well, backwards. That's cernuation.
As I wrote before, I admire the ingenuity that went into its design. The more I think about it though, the more I start doubting how well it would work. There is no mechanical problem at all in swinging like this. Instead, the problem is one of motor control and of visual perception. It is amazing that animals like gibbons actually manage to travel through woods at high speeds. Just imagine how much more difficult their task would be if their image of the world not just zoomed forwards as well as bobbing up and down, as it does in brachiation, but also rotated constantly as it must in cernuation. Have a look at the animal's head above: it is actually turned upside down at one point. How do cernuating animals manage to pick out the next branch?
Click to enlarge; copyright Gert van Dijk
That must have been the reason why the squibbon's designers situated its eyes near the centre of mass. The picture above shows all stages in the movement, with a black line indicating the position of the eyes. Compare that to the position of the feet or the hands (blue line), and you will see that the centre of the body moves less vertically than any part far away from the centre. You may now also understand why the squibbon's eyes stick out sideways: if not, it would not be able to look forwards at times because its body would be in the way!
Click to enlarge; copyright Gert van Dijk
While this eye position minimises vertical displacement, it does nothing to solve the problem of the eye rotating, and with it the animal's view of the world. Perhaps that can be rectified. Let's suppose the head can be rotated by about 180 degrees. Have a look at animal A shown here. Hanging from its hands like this it will view the world as being the right side up. If it were to change the position of its head as in B, it would see the world upside down, right? That is not at all useful, unless of course the body itself would be upside down. Obvioulsy that is the case while cernuating, so if we take animal B, freeze it and rotate it, head and all, you get animal C. The trick would be for the animal to rotate its head from one position to the other quickly when the point of contact changes. During the swing, the animal could then always keep the head in the same vertical position so it could see what it is doing! I do not know whether squibbons were supposed to this by rotation of the eye stalks, but why not...
Mind you, I think brachiation is by far the easier solution, and I do no intend to fill Furahan forests with screeching cernuators. Still, it is interesting to think about, isn't it?
This is probably the point where the rift between those who say 'yes' and the vast majority of mankind is revealed...
Brachiation is what comes to mind when gibbons or monkeys swing from branch to branch: they hang from one arm while the other swings to grab another branch. While they do so the body stays largely upright, meaning the head is always above the feet.
The way squibbons do this, cernuation, has similarities: the animal swings suspended from one or more arms while other arms move forward to grab a new branch. But the movement is like an inverted somersault, so, while one swing sees the head upwards, the next has it downwards. I presented a fragment of 'TFIW' showing a squibbon moving that way, but the lighting was not very even so the movement may not have been well visible. This post rectifies that.
Click to enlarge; copyright Gert van Dijk Above you see a rough model of a cernuator. It is only a simple ZBrush model, not meant as a proper animal (I hope my ZBrush friends will forgive me). The animal has very long eye stalks, long arms and long legs, and the head is kept downwards so the eyes stay near the centre of the body; the body is even bent to make room. Having the eyes near the centre was borrowed from the squibbon; this particular concept is stressed in the book 'TFIW'. The idea is probably that this eye position minimises the vertical distance the eyes travel over during cernuation. We'll get back to that.
Click to enlarge; copyright Gert van Dijk 
Click to enlarge; copyright Gert van Dijk
Click to enlarge; copyright Gert van DijkAnd finally the animal swings from its hands right up to the point where the cycle began. Notice that the body is now right side up again, and the back faces, well, backwards. That's cernuation.
As I wrote before, I admire the ingenuity that went into its design. The more I think about it though, the more I start doubting how well it would work. There is no mechanical problem at all in swinging like this. Instead, the problem is one of motor control and of visual perception. It is amazing that animals like gibbons actually manage to travel through woods at high speeds. Just imagine how much more difficult their task would be if their image of the world not just zoomed forwards as well as bobbing up and down, as it does in brachiation, but also rotated constantly as it must in cernuation. Have a look at the animal's head above: it is actually turned upside down at one point. How do cernuating animals manage to pick out the next branch?
Click to enlarge; copyright Gert van Dijk
Click to enlarge; copyright Gert van DijkWhile this eye position minimises vertical displacement, it does nothing to solve the problem of the eye rotating, and with it the animal's view of the world. Perhaps that can be rectified. Let's suppose the head can be rotated by about 180 degrees. Have a look at animal A shown here. Hanging from its hands like this it will view the world as being the right side up. If it were to change the position of its head as in B, it would see the world upside down, right? That is not at all useful, unless of course the body itself would be upside down. Obvioulsy that is the case while cernuating, so if we take animal B, freeze it and rotate it, head and all, you get animal C. The trick would be for the animal to rotate its head from one position to the other quickly when the point of contact changes. During the swing, the animal could then always keep the head in the same vertical position so it could see what it is doing! I do not know whether squibbons were supposed to this by rotation of the eye stalks, but why not...
Mind you, I think brachiation is by far the easier solution, and I do no intend to fill Furahan forests with screeching cernuators. Still, it is interesting to think about, isn't it?
This is probably the point where the rift between those who say 'yes' and the vast majority of mankind is revealed...
Subscribe to:
Posts (Atom)
