In a previous post on scaling I tried to explain why you cannot simply double all size measures of an animal if you want to make it bigger. Leg bones in particular should become more than twice as thick. The reason was that doubling an animal's length, height and width will make it weigh not two but eight times as much. To withstand the eightfold increase in weight the cross section of the leg bones has to become eight times larger, instead of four times, which is what you get if you merely double the diameter. The wanted diameter change is obtained by taking the square root of how much the cross section has to change. The square root of 8 is 2.82, so there we are.
All that held for altering an animal's size on one and the same planet; but what happens if the animal's size is kept the same, but it is transferred to a world with a different gravity? This is easy: the leg bones once again have to withstand the weight of the animal, so the question is how much that changes under the influence of another gravity. Weight is a force: it is the product of the gravitational acceleration g and the object's mass. From that it follows that weight is directly proportional to the value of g, and that value depends on the planet; Earth's gravity is taken as the standard, so it is at 1g. Transporting a animal of any given weight to a 2g world will double that weight, and being on a 3g world will triple it, etc. To adapt its bones to these new environments, their cross section will have to become twice as large on a 2g world, three times as large on a 3g world, etc. What that means for the diameter of the bones is not difficult to work out: for the 2g world the original diameter has to multiplied by the square root of 2, which is 1.41, and for the 3g world the value would be the square root of 3, or 1.73.
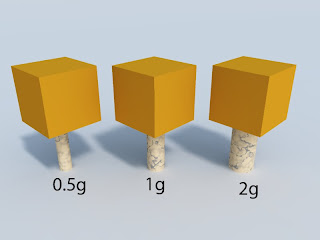
The picture above shows a mass on a cylinder. The diameter of the cylinder is just right to support the weight of the cube. The cubes are thought to stand on three different worlds, with 0.5g, 1g and 2g. The cylinders have been changed to make them right for each world, so their diameters are 0.70, 1, and 1.41.
For the mathematically inclined here is the relationship between body size, leg bone diameter and gravity, all together. The change in overall size you want to achieve is given on the x-axis (so '3' means the animal's height, length and width are all to become three times the original size), and the y-axis shows by how much you have to multiply the original leg bone diameter to obtain the new one. The three blue lines give the relationship for three different values of g. Suppose that your animal will run into trouble if the bone diameter increases beyond four times, for instance because too much of the animal will be bone! The graph shows that you reach that diameter value when the size increases a bit more than two times on a 2g world, but on a 0.5g world the animal can become more than three times the original size. So you can have animals with thin bones on a heavy planet, but they just have to be rather smaller than animals with similar bones on a low-gravity planet.
Finally here is the cartoon doggie (Disneius caniformis) adapted to three different worlds. Of course, there are other things to take care of when designing life forms for worlds with different gravities. While an animal's weight changes by transporting it to another world, its mass does not, and its inertia does not either. Muscle mass will need to be changed as well, as withstanding a greater weight will require larger muscles. Leg position may have to be changed as well. The more difficult it is to counter a high weight, the more likely it is that the legs will be kept vertically, i.e., without major angles between the bones. The difficulty in question depends both on an animal's mass and on local gravity. Mind you, there is more to be said on leg bending, as well as on leg splaying; the two are not the same thing, but perhaps that is something for another post.
PS. It seems to be getting more difficult to find new interesting speculative biology projects out there that aren't well-known already. I have my eye on one, but suggestions are welcome.
Sunday, 18 July 2010
Subscribe to:
Post Comments (Atom)


10 comments:
Very clearly written.
I hope this series continues long enough to discuss the relationship between gravity, atmospheric pressure and *flight* -- which i confess is a little beyond me.
Yes, it would be rather interesting to be able to find relationships for bones for flight on different planets, as the honeycomb structure on earth might not be needed for a planet with lesser gravity.
Wonderful post!
Thank you, JW, SingYu and Brynn.
I was afraid that writing posts of such a technical nature might frighten readers away; after all, not everyone enjoys mathematics.
Apparently, I was wrong, at least as far as some people are concerned. I intend to write similar posts from time to time, but it is much easier to think of questions than to answer them...
OK, let's see if i understand these relationships:
Some people have estimated that 100,000 pounds is as big as a land-dwelling tetrapod vertebrate could get on earth. Let's assume that this is true.
How would this compare to the size limit of other planets for instance a .5G and 2G planet? On the .5G planet it would take twice the mass to make 100,000 pounds, and on the 2G planet half the mass would be required.
So it seems to me that 100,000 pounds as measured on a given planet would be the maximum size no matter what the gravity is.
Is this correct, or am i missing something?
Of course inertia is not subject to gravity, so there might be additional constraints on the size of huge low-gravity creatures i.e. they couldn't stop or start quickly or inertia would tear them apart.
P.S. I think you are already aware of "Life on Nereus"
http://temp.evanblacknet.officelive.com/nereidlife.aspx
JW: I will get back to that tomorrow ('pounds'?). Did you get the estimate from an internet source I could have a look at?
I think you are right: if the maximum estimate is based on limits posed by total bone or muscle mass, then indeed the total mass can be higher on a low gravity world, as that will lower the proportion of total mass taken up by muscle and bone. I could work that proportion out if it is interesting.
Mind you, a low gravity biotope such as the sea proves your point nicely: a blue whale has enormous mass and very low weight. I tried to find its mass, but was stumped by 'tons' and 'tonnes'. Metric is really so much easier...
I know Evan's work, and have emailed with him; we'll wait for an upgraded site.
I'm not really arguing that the 100,000 pound limit is correct. I'm just trying to understand how the maximum possible size of a land-dwelling animal (of a given type) would vary with gravity.
As for the 100,000 lb estimate, i've seen an estimates for maximum possible sauropod size that range between 90,000 Kg and 900,000+ Kg. But unfortunately any of the information about how that estimate was arrived at has been behind a pay wall.
The largest weighed blue whale was 190,500 kg, though longer, unweighted whales are known.
Sigmund: I could work that proportion out if it is interesting.
Yeah i think that would be rather valuable.
Among other things i'm working on a "tool" to randomly create novel alien creatures, as an aid to help creature designers get beyond their preconceptions. It currently has a rather simplistic connection between gravity and creature size.
You can see what i currently have here:
http://s1.zetaboards.com/Conceptual_Evolution/single/?p=563602&t=3600674
Have you heard of Affex? It's one of my favorite speculative biology projects, and not that well known:
http://zippo4k.deviantart.com/gallery/#AFFEX
I plan to have an upgraded site, but it may be some time in the future. If you're set on waiting for the new site, you're in for a long wait.
well, as far as I know, if a terrestrial animal had 130 000 kg (that would be 130 metric tons?) I'm not really familiar with those as they are completely foreign to me, we have only one ton in my country and that is precisely 1000 kg. xxD
Anyway. if an animal here had 130 tons its legs would be so thick they would rub each other and the animal could not walk, I think 100000 pounds is way too underestimated, given that 2 kg is roughly five pounds if i recall correctly, but my data comes from an old source, and many dinosaurs have been re-estimated to weight much less than previously thought, but I guess this number (the 130 t) did not have anything in common with dinosaurs specifically, and if there was a study, and this is the number they came up with, it seems reliable to me. It comes from Stephen Jay Gould's "The Book of Life"
Post a Comment